We all know the usual jokes about the ‘S’ in ‘IoT’ standing for ‘Security’. It’s hardly a secret that security in embedded, networked devices (‘IoT devices’) is all too often a last-minute task that gets left to whichever intern was unfortunate enough to walk first into the office that day. Inspired by this situation, this is absolutely not the case in blockchain applications since data integrity is crucial for it
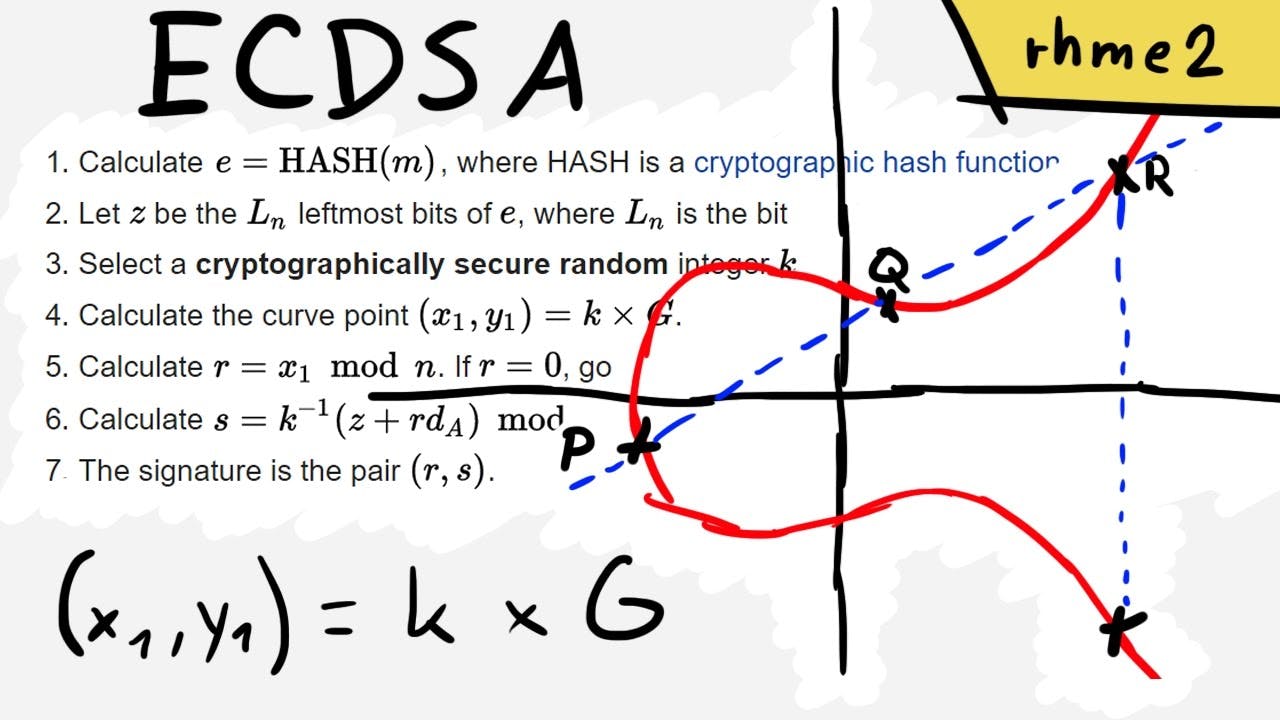
Elliptic Curve Cryptography (ECC) is an encryption technique that provides public-key encryption similar to RSA. While the security strength of RSA is based on very large prime numbers, ECC uses the mathematical theory of elliptic curves and achieves the same security level with much smaller keys.
Public-key cryptography is based on the intractability of certain mathematical problems. Early public-key systems based their security on the assumption that it is difficult to factor a large integer composed of two or more large prime factors. For later elliptic-curve-based protocols, the base assumption is that finding the discrete logarithm of a random elliptic curve element with respect to a publicly known base point is infeasible: this is the "elliptic curve discrete logarithm problem" (ECDLP). The security of elliptic curve cryptography depends on the ability to compute a point multiplication and the inability to compute the multiplicand given the original and product points. The size of the elliptic curve, measured by the total number of discrete integer pairs satisfying the curve equation, determines the difficulty of the problem.
In practice, ECC is often used with Diffie-Hellman to speed up performance. ECC does not replace RSA for authenticating the communication partners but is used for generating the ephemeral DH session key with the help of an EC private key. RSA is still used for providing authentication. The related SSL cipher suites all have ECDHE-RSA in their names and complement the plain DHE-based cipher suites. The main advantage of Elliptic Curve Cryptography with Diffie-Hellman (ECDHE-RSA) over plain Diffie-Hellman (DHE-RSA) is better performance and the same level of security with fewer key bits. A disadvantage is an additional effort for creating and maintaining the EC key.
Elliptic curve ciphers were first proposed independently by Victor Miller and Neal Koblitz in the mid-1980s. At a high level, they are analogs of existing public-key cryptosystems in which modular arithmetic is replaced by operations defined on elliptic curves. As with all public-key cryptosystems, the security of elliptic curve cryptosystems relies on difficult mathematical problems at the core. Given two points G and Y on an elliptic curve such that Y = kG (ie, Y is G added to it k times), find the integer k. This problem is often called the elliptic curve discrete logarithm problem. Currently, general methods of calculating discrete logarithms of elliptic curves are much less efficient than traditional methods of factoring or calculating discrete logarithms.
Elliptic curves are not ellipses. They are named that way because they are represented by expressions similar to the cubic equations used to calculate the circle of an ellipse. If we consider a K field, it can be K, R Real numbers, Q Rational numbers, C- Complex numbers, or if we assume that p is a prime number, it can be Fq -finite field consisting of q=pr elements. The characteristic of the finite field GF(2) is 2, and the characteristic of real and complex numbers is infinity
Integer Factorization Using Elliptic Curves
In 1987, Hendrik Lenstra published the landmark paper that introduces and analyzes the Elliptic Curve Method (ECM), which is a powerful algorithm for factoring integers using elliptic curves.
Lenstra’s method
The Lenstra elliptic-curve factorization or the elliptic-curve factorization method (ECM) is a fast, sub-exponential running time, algorithm for integer factorization, which employs elliptic curves. For general-purpose factoring, ECM is the third-fastest known factoring method. The second-fastest is the multiple polynomial quadratic sieves, and the fastest is the general number field sieve.
The Lenstra elliptic-curve factorization is named after Hendrik Lenstra.
Practically speaking, ECM is considered a special-purpose factoring algorithm, as it is most suitable for finding small factors. Currently, it is still the best algorithm for divisors not exceeding 50 to 60 digits, as its running time is dominated by the size of the smallest factor p rather than by the size of the number n to be factored. Frequently, ECM is used to remove small factors from a very large integer with many factors; if the remaining integer is still composite, then it has only large factors and is factored using general-purpose techniques.
The largest factor found using ECM so far has 83 decimal digits and was discovered on 7 September 2013 by R. Propper. Increasing the number of curves tested improves the chances of finding a factor, but they are not linear with the increase in the number of digits.
Lenstra’s algorithm is well suited for finding “medium-sized” factors of an integer N, which today means 10 to 20 decimal digits. The ECM method is not directly used for factoring RSA challenge numbers, but it is used on auxiliary numbers as a crucial step in the “number field sieve”, which is the best-known algorithm for hunting for such factorizations. Also, the implementation of ECM typically requires little memory.

